Project Description
Numerical simulation of instabilities in gas-liquid interfases
The triggering and development of instabilities at the separating surface (interface) between two streams of liquid and a gas, downstream of dividing plates with infinitesimally thin and thick train edges are studied in this Thesis. The mixing layers between two flows of liquid an gas, as well as this liquid sheet injected between two gas coflows are analyzed. Arbitrary initial perturbations are not imposed and the systems naturally develop instability, depending on the geometric characteristics and the flow parameters.
Studies conducted by others investigators are described and the governing equation is derived in a correct dimensionless form. The Reynolds numbers of the gas and liquid flows, the momentum flux ratio (or equivalently, dynamic pressure ratio), the velocity ratio of the two streams and the ratio of the momentum thickness for the two flows (or generally speaking, of two characteristic lengths in a direction perpendicular to the mean velocities) are the key dimensionless groups. A geometric dimensionless parameter based on the plate thickness and other characteristic length appears in the finite thickness cases.
In the numerical solution of the equations of motion, the finite volume technique and the commercial code PHOENICS are utilized, with special emphasis on the use of high order accurate schemes for the discretization of the temporal and convective terms. For all the cases considered the two-dimensional Navier-Stokes and continuity equations for both fluid phases treated as incompressible, are solved. The equations for the two phases are coupled through the kinematic conditions and those expressing normal and tangential stress balances at interfaces. For single phase flows, a transport equation for the mixture fraction is also included.
Subroutines are added to the code for the treatment of two phase flows; they are designed as a part of this work and incorporate to the numerical solution the method known as Volume of Fluid (VOF), in order to locate and follow the liquid-gas interface, the method named Continuum Surface Force, to model the effects of the surface tension force and alternating direction techniques for the time integration.
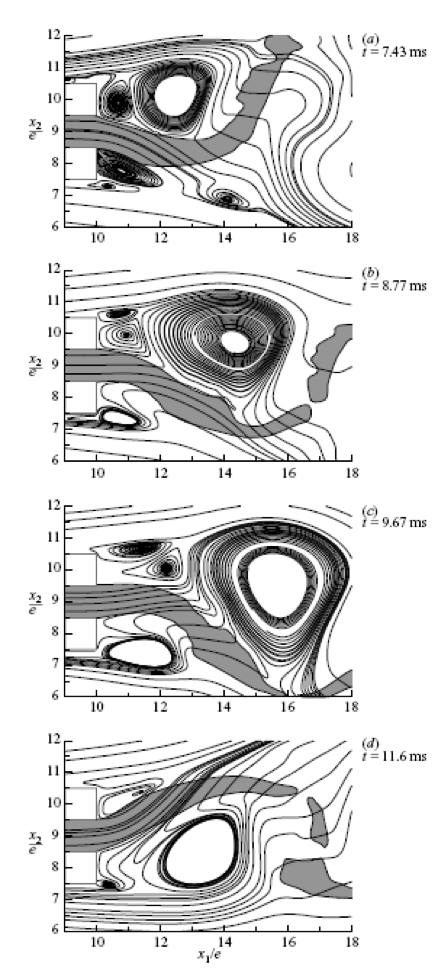
As a part of the implementation and validation of this mathematical tool to simulate the flow downstream of plates with infinitesimally thin or thick trailing edges, the mixing of lows of the same fluid and of fluids with slightly densities are treated for the four injection geometries already mentioned. The typical vorticity structures in a single phase mixing-layers and wakes are reproduced as well as the correct trend for the variation of Strouhal numbers as a function of Reynolds number behind a thick trailing edge.
The liquid-gas interface behavior in a mixing layer behind a solid plate of non_negligible thickness for several gas flow Reynolds numbers is studied. The results show the formation of vorticity structures in the near wake and the direct relation between the pressure fluctuations induced by those structures and the development of interface instabilities. These instabilities grow, generating filaments which in turn interact with those structures modifying the wake dynamics, the influence being greater for higher coflow Reynolds numbers. Moreover, the application of the Navier slip-condition for the interface/solid contact line does not significantly alter the interface evolution, at least for the values of the slip-coefficient employed. The displacements of the contact line and the variation of the contact angle seem to be narrowly connected to with the large fluctuation of the fluid fields in its neighborhood, which only take place, for the cases analyzed, as the starting flows reach the plate trailing edge in their initial unsteady development.
The instability of a thin liquid sheet surrounded by two symmetric gas coflows is also investigated. The system behavior, as the streams momentum flux ratio is varied, is analyzed. The effect of the surface tension force at the interface is evaluated. Likewise, the influences of the contact lines slip condition, of the liquid exit velocity profile and of the solid plates chickeness on the liquid sheet oscillation characteristics are studied.
The results display the dynamics of both phases downstream of the plates trailing edges, in the neighborhood of the injection, and the gas flows influence on the interface. The vortex shedding in the gas phase determines the pressure and velocity fields which cause the oscillation and the deformation of the liquid sheet and fix, among other characteristics, its oscillation frequency and wavelength of the developed perturbation. For momentum flux ratios of order unity or larger, the liquid sheet oscillation frequency notably approaches that of gaseous vortex shedding. Under all circumstances, the phase velocity of the developed perturbation approximately maintains a constant value, as predicted by linear stability theory. For the cases analyzed, the surface tension force does not sensibly vary the liquid sheet oscillation frequency or the wavelength; however, the distance of intact sheet, with no large deformations, seems to increase and the interaction of the vortical structures generated on both sides of the sheet seems to be more intense. This interaction allows the development of other oscillation modes. On the other hand, the application of the Navier slip-condition to the contact lines decreases the sheet oscillation frequency, with no change of the phase speed. Different liquid-phase exit velocity profile modifies the dynamics of both phases in the neighborhood of the injection and the values of the oscillation frequency and the wavelength, with no significant alterations of the phase velocity. Finally, an infinitesimally thin plate change the sheet oscillation frequency values with respect to those for a thick plate, but do not modify the phase speed or the global process dynamics.