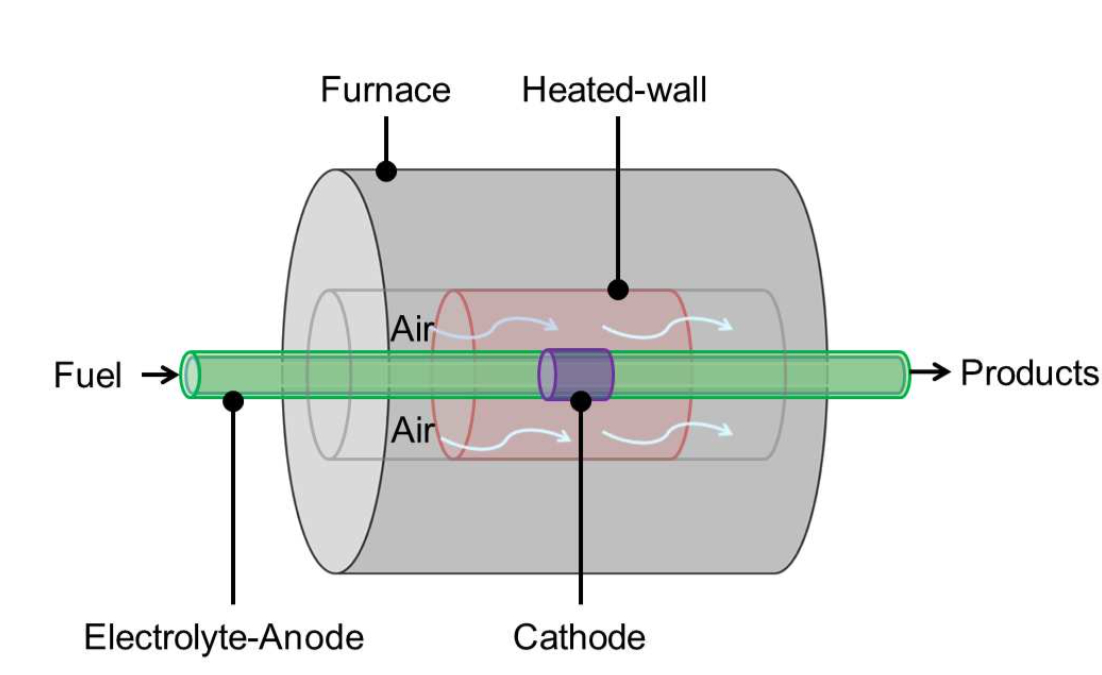
Project Description
This Thesis presents a comprehensive mathematical model that describes the perfor- mance of a hydrogen-fed, self-supported solid-oxide fuel-cell, and the corresponding numerical method to solve the model. The latter has been implemented using an open-source CFD-toolbox, OpenFOAM. The validity of the resulting numerical tool has been shown by comparison of its results with experimental data taken from the literature, and its applicability has been illustrated in a further numerical analysis.
The mathematical model for the description of the solid-oxide fuel-cell performance consists of a set of submodels describing the multiphysics nature of the solid-oxide fuel-cells. Thus, the model is subdivided into:
- The channel model, which describes the physical phenomena taking place within any of the two channels of a single SOFC. Hence, it accounts for the mass-, momentum-, species- and heat-conservation equation within the chan- nels.
- The electrode model, which consists of a set of equations that accounts for the global mass transfer and the heat transport within any of the SOFC electrodes, cathode or anode.
- The electrolyte model, required to model those phenomena occurring within the impervious electrolyte of the solid-oxide fuel cells. It thus takes into account both heat and charge transport.
- The electrochemical model, that accounts for the electrochemical reactions taking place at triple-phase-boundaries of the SOFCs, which are the driving force in the operating principle of these devices.
- The radiation model, to account for the surface-to-surface radiative heat exchange.
With respect to other models published in the literature, the present one has the following salient features:
- In the channels, a consistent multicomponent diffusion model is used. Hence, the species conservation-equation in the channels is solved for all the species in the gas mixture, avoiding the artificial imposition of the diffusive-flux consistency that is needed when the widely used Fickian law for multicomponent mixtures is employed.
- The global mass transfer within the porous electrodes is modelled with the dusty-gas model of Mason and Malinauskas, that is reported as the most suitable one for modelling this type of mass transport. It accounts for all the possible transfer mechanisms that can arise in a porous medium, ie ordinary diffusion, Knudsen diffusion and viscous flow; this is unlike most of the published models, that usually neglect the viscous flow within the electrodes.
- A novel mathematical treatment of the dusty-gas model equations is presented in this work. The complex system of equations of the DGM is formulated as a Navier-Stokes-like equation for the species transport that is easier to include and to solve in a standard CFD code than the original formulation.
- The conjugate heat transfer within the cell is addressed using the sensible enthalpy conservation equation throughout the whole SOFC system. This equation has been properly formulated in terms of temperature, so the dependence on temperature of the specific-heat at constant pressure of the fluids is not neglected, while at the same time the equation is consistent with this dependence.
- Conjugate heat transfer, mentioned above, is modelled considering all heat-transfer modes, including radiation, which is often neglected or highly simplified in the SOFC modelling literature. The surface-to-surface radiative heat transfer is modelled using a view-factor method that accounts for both parallel and oblique radiation between the radiative surfaces of the system.
The numerical method consists of a numerical algorithm, embodying other subroutines for the numerical solution of the SOFC mathematical model. The algorithm has been developed in-house and has been implemented using the finite-volume libraries available in OpenFOAM, an open-source CFD-toolbox. The main features of this numerical method are:
- The numerical domain is split into five adjacent numerical subdomains, that facilitate the solution of the proper model in each of the SOFC layers; namely: (1) the fuel channel; (2) the anode; (3) the electrolyte; (4) the cathode; and (5) the air channel. This implies that the numerical solution is calculated in five separate numerical meshes.
- The spatial multidomain nature of this solution procedure requires of an algorithm to exchange information between adjacent subdomains. The subdomain coupling is done, in this work, either by mapping field between adjacent sub- domains or by using a coupled solver.
- The numerical algorithm can be run in parallel.
Parts of this numerical algorithm, viz those subroutines embodying species mass-transfer within the channels and electrodes, have been included in an open-source mass-transfer library that has been submitted for public release.
The validity of the numerical tool has been verified by comparing the experimental results of Campana et al. for a hydrogen-fed anode-supported SOFC with the corresponding numerical results. The numerical tool has been further used to characterize in detail the mass-transfer process within the porous media, as well as to investigate the suitability of some common assumptions made in other SOFC modelling works. The main topics of this further analysis are:
- The novel mathematical treatment of the dusty-gas model equations that is presented in this work explains the mass transfer within the electrodes as consisting of three distinct contributions, called DGM fluxes. The physical meaning and the relevance of these DGM fluxes has been studied.
- The classical point of view for the mass-transfer phenomena, consisting of mass diffusion (including ordinary and Knudsen) and mass convection, is also considered in this work. Since convection is often neglected in other SOFC modelling works, a numerical and analytical studies to evaluate the relevance of the convective term in the global mass transfer process has been presented.
- The classical and the dusty-gas model descriptions of the pressure driven mass-flux, ie convective and the pressure-driven DGM flux, have been compared, and an analytical study of the relevance of the latter on the global mass-transfer phenomenon has been performed.
- The suitability of the common assumption, often found in the literature, stating that the temperature of the reactant streams entering the SOFC is equal to that of the preset operating-temperature, has been questioned in this work.
- The relevance of the surface-to-surface radiative heat transfer, often neglected, in the conjugate heat transfer within the SOFC system has been evaluated.
- The validity of the 1-D approach to model the charge transfer within very thin electrolytes has been studied.
The main conclusions of the above analysis are summarised below:
- The mass transfer of both reactants and products within the SOFC electrodes is dominated by an effective diffusion and is hindered by the counterflow of the other species. For the reactant, an additional resistance to mass transfer appears due to an effective flow caused by the pressure gradient. On the contrary, this pressure-gradient benefits the evacuation of the product from the reaction sites.
- Convective mass-transfer may represent a non-negligible part of the global mass transport within the SOFC electrodes, under certain operating conditions.
- The magnitude of the pressure-driven DGM flux is generally smaller than that of the convective flux. However, neither of them are negligible for large pore sizes, or when operating at medium to high fuel concentrations, at high pressures or low temperatures; which, in fact, are the desired operating conditions for efficient and economical SOFCs.
- The reactant streams may cool down the system, and deteriorate the SOFC performance, if their temperatures do not reach the preset operating-temperature as they approach the cell active areas.
- Surface-to-surface radiation within the cell surface and the channel surfaces is relevant in the global heat transfer within the SOFC, and thus it should not be neglected.
- The electrochemical characterization of the SOFC electrodes is of major significance for the proper applicability of the SOFC CFD.
- The charge transport through very thin electrolytes is quasi 1-D.